La gravetat segons Dragon Ball

Com ja hem vist molts cops en els còmics i la televisió solen haver-hi fenòmens científics dignes d'estudi, per desgràcia no hi ha gaire gent disposada a fer aquesta anàlisi, així que em toca a mi (que ni tan sols sóc estudiant de física) fer la feina bruta, molt bonic, sí senyor...

Això sí, en aquesta entrada no només estudiaré la física aplicada a aquesta sèrie, sinó que a més em centraré únicament en els fenòmens gravitatoris.

El planeta Kaito: en aquest petit planeta hi ha una gravetat 10 cops superior a la de la Terra, normal que quan en Goku hi arriba per primer cop gairebé no pugui caminar. Però tot seguit, veurem que caminar hauria estat el menor dels seus problemes. He comptat que el planeta Kaito té un radi d'uns 21 metres, amb aquest radi hauria de tenir una massa de 6500 bilions de kilos per a poder originar una atracció gravitatòria 10 cops més gran que la de la Terra. Potser aquesta dada sembla poc important, però què passa si us dic que aleshores el planeta Kaito tindria una densitat de 1,67·10^8 g/cm3? A l'univers, els únics cossos amb densitats semblants són les nanes blanques, estrelles que han quedat sense "combustible" i es van reduïnt en tamany i condensant-se. El cas és que a la superfície de les nanes blanques la temperatura no baixa d'uns 10.000 graus, cosa que sembla estranya ja que mai he vist suar al rei Kaito.

Un món sense lluna: el primer cop que els nostres herois s'enfrenten a en Vegeta veuen que aquest pot obtenir cert poder provinent de la lluna, així que decideixen destruïr-la (la cosa més normal del món), després d'anihilar el satèl·lit sembla que no passi res, el problema és que SÍ que passaria, i en passaria una de molt grossa. I és que el sistema solar està en un equilibri molt delicat, una petita variació en algun dels seus elements i es trencaria l'equilibri gravitatori, la destrucció de la lluna afectaria l'òrbita de la terra i aquesta, la de la resta de planetes, fet que segurament acabaria amb l'existencia de tot el sistema solar, així que, siusplau, la lluna no la toquem massa.

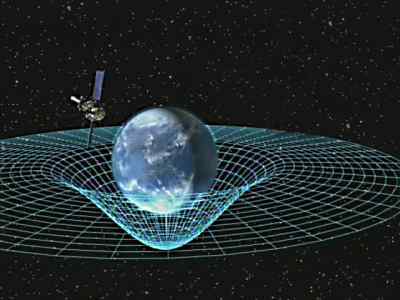
Un vell conegut: tot i que ja ho vaig posar en una altra entrada no puc deixar de remarcar que el fet que en cada combat els lluitadors passin hores mirant-se també és un efecte de les lleis gravitatòries. Segons la teoria de la Relativitat els cossos deformen l'espai-temps de manera proporcional a la seva massa, tenint en compte la fórmula E=m·c^2 podem intuir que la massa d'un superguerrer de Dragon Ball és enorme, ja que té energia suficient per destruir planetes com si res; d'aquesta manera els nostres lluitadors crearien una gran deformació a l'espai-temps fent que el que passa dins la zona de la seva influència gravitatòria es percebi per un observador exterior d'una manera molt més lenta.
I aquí acaba el post d'aquesta setmana, sóc conscient que per parlar de Dragon Ball algú em criticarà o titllarà d'heretge però, què hi farem? Per últim agrair a alguns amics certes idees, ah, i com us dic sempre...

Superherois atòmics

Aquest cop, a petició d'un amic meu, parlaré dels superherois, almenys de la part que pugui analitzar una mica. I és que més d'un cop aquests musculosos homes ens han sorprès amb extravagàncies o incongruències que han cridat la nostra atenció. Comencem sense més dilació.

Hulk: la veritable identitat de "la massa" és la del doctor Bruce Banner, un eminent físic nuclear que treballava en la bomba gamma. Però un dia, el nostre amic va tenir la mala sort de ser víctima d'una explosió d'aquesta bomba, i això el va convertir en Hulk. El primer error el trobem recorrent a la dosimetria, la ciència que estudia l'absorció de radioactivitat en organismes vius. En concret, per un humà, la dosi mortal és de 10 Sv (1Sv=1J/1Kg) en el 100% dels casos. Aleshores, com expliquem que Bruce Banner sobrevisqués a l'explosió? Senzillament, no hi ha explicació aparent.

Però encara hi ha una altra incògnita interessant respecte al "colós verd". En la seva forma de Bruce Banner té una massa de 60kg, mentre que quan es transforma en Hulk passa a pesar 450kg, com pot ser? A l'escola sempre m'han explicat que la matèria no es crea ni es destrueix. És cert que la massa es pot transformar en energia i viceversa, però quan el nostre amic verd passés de ser Hulk a un vulgar humà alliberaria uns 108.000 milions de Joules creant una explosió que ho destruiria tot a kilòmetres a la rodona.

Dr. Manhattan: l'origen d'aquest personatge és molt semblant a l'anterior: Jon Osterman és un físic que treballa en experiments relacionats amb el "camp intrínsec" (un camp fictici). Un dia que semblava com qualsevol altre, el pobre doctor queda tancat dins la màquina que desfà els camps intrínsecs (segurament una barreja de força electromagnètica i forces nuclears) i queda reduit a no-res, no en queda ni un àtom del pobre vailet. Tot i això, un temps després el dr. Osterman resucita sota la forma d'un personatge blau a qui els medis informatius bategen com a Dr. Manhattan, un "ésser" capaç de manipular la matèria a nivell atòmic. Doncs aquí el tema no pot estar més clar, és absolutament impossible que tots els quarks i electrons (ni tan sols àtoms!) que havien format part de Jonathan Osterman s'uneixin de nou, i molt menys que s'uneixin creant a un individu amb la personalitat del doctor, però amb aspecte diferent. Com no podia ser d'altra manera el Dr. Manhattan és un gran personatge per analitzar fenòmens físics, ja que pot teletransportar-se i veure el passat i el futur.

La seva capacitat de teletransportació no és molt difícil d'explicar, encara que poca gent ho sàpiga, ja és possible teletransportar àtoms individuals gràcies a l'entrellaçament quàntic, tenint en compte que el doctor pot manipular la matèria a nivell atòmic no sembla una cosa gaire inversemblant. D'una manera semblant també es pot trobar una explicació a la seva capacitat per "veure a través del temps", doncs per algú amb les seves capacitats no deu ser difícil captar els neutrins, unes partícules subatòmiques que es sospita que poden viatjar endavant i enrere en el temps.

Fins i tot i ha una explicació al fet que emeti aquesta llum blava. La resposta és l'anomenada radiació Cherenkov, la radiació de color blau típica dels reactors nuclears, que es produeix quan un electró (o una partícula amb càrrega elèctrica) es desplaça a través d'un medi a una velocitat superior a la de la llum (en aquell medi), no donaré més detalls perquè és un procés força complicat i cal tenir coneixements d'electromagnetisme.

Per cert, no us sembla que ser físic no és gaire bon negoci? A un li explota una bomba atòmica a la cara i a l'altre el desintegren! Bé, amb això m'acomiado per avui, sóc conscient que l'entrada d'avui és una mica complicada però es fa el que es pot...

Errors en ficció clàssica

A l'entrada d'avui s'intentarà trobar errors en alguns dels elements de ficció més arrelats i estimats per la societat, així que he de fer una advertència: aquest post pot ferir la sensibilitat dels amants de la ciència-ficció o de la ficció més clàssica (elfos, dracs i frikades semblants).

Les ales d'un drac: generalment els dracs són representats com uns rèptils alats, d'uns 15 o 20 metres de longitud, són capaços de llançar foc pels queixals i, fins i tot, de volar, tot i que això últim no està tant clar. Un drac d'uns 15 metres pesaria unes 10 tones (aproximadament), aleshores quan vola la seva força de sustentació hauria de ser igual al seu pes, però perque això fos possible les seves ales haurien de tenir una mida determinadada. Què quina mida seria? Doncs després de calcular-la he trobat que cada ala faria uns 13.783 metres quadrats. Ja que el tema era ficció clàssica també he pensat en unes criatures encara més clàssiques que els dracs, els àngels. Utilitzant el mateix mètode d'abans he descobert que per que un àngel pugués volar necessitaria unes ales de 11 metres quadrats, Déu n'hi dor.

Làsers a Star Wars: el cas és que un dispar láser mai es veuria a l'espai, ara ho explico. La llum viatja per l'espai fins xocar amb algún cos. Quan la llum es troba amb algun cos material es reflecteix, i això és el que nosaltres veiem: el cos absorveix llum de totes les longituds d'ona possible exepte d'una, aquesta llum que no absorveix és reflectida i nosaltres la captem i la interpretem com el color. Hem de saber que el láser és un feix de llum amb una bona quantitat d'energia, si aquesta llum no troba un medi material on reflectir-se no la veurem i com a l'espai hi ha el buit absolut, pues aquí ho tenim, mai podríem veure el feix de llum. Això per no parlar del tema que la llum viatja a 300.000.000 metres per segon i ens seria impossible veure le moviment del raig luminós.

El sabre làser: em sap greu ficar-me amb el sabre làser, la millor arma de la galàxia i part de l'extranger, però tranquils, més que un error científic és un error de nomenclatura. Potser algun cop us heu preguntat com s'ho fan per crear un feix de llum d'una longitud determinada, teòricament no es pot delimitar una secció de llum. Doncs el tema és que no és un sabre làser, és un sabre de plasma. El fonament científic és elevar la temperatura d'un gas per sobre dels 30.000 Cº, fins al punt que els electrons es dissocien i es torna plasma, després és concentra l'energia cinètica del gas en un punt i s'aconsegueix una cosa semblant al sabre làser, senzillament apostoflant.

Ufff, fins aquí el post d'avui, tal i com diria Michael Robinson a las noticias de Giñol: "hasta aquí pescao vendido, no se olviden de reír y etcétera etcétera para todos". Un moment, hi ha un altre personatge il·lustre que vol acomiadar-se...